Generalized arithmetic progression
In mathematics, a multiple arithmetic progression, generalized arithmetic progression, or k-dimensional arithmetic progression, is a set of integers constructed as an arithmetic progression is, but allowing several possible differences. So, for example, we start at 17 and may add a multiple of 3 or of 5, repeatedly. In algebraic terms we look at integers
- a + mb + nc + ...
where a, b, c and so on are fixed, and m, n and so on are confined to some ranges
- 0 ≤ m ≤ M,
and so on, for a finite progression. The number k, that is the number of permissible differences, is called the dimension of the generalized progression.
More generally, let
be the set of all elements  in
in 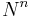 of the form
of the form
with 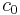 in
in  ,
,  in
in  , and
, and  in
in  .
.  is said to be a linear set if
is said to be a linear set if  consists of exactly one element, and
consists of exactly one element, and  is finite.
is finite.
A subset of 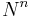 is said to be semilinear if it is a finite union of linear sets.
is said to be semilinear if it is a finite union of linear sets.